探索的因子分析の際の平行分析について
はじめに
因子分析に関連した調べ物の必要があって,その覚書。今回は平行分析について。
探索的因子分析で因子数を決めるための複数の基準が提案されていますが,平行分析(parallel analysis)はその一つで,因子分析の教科書などでも勧められる方法です。アイデアとしては,分析しようとしているデータセットと同じサイズであるランダムなデータセットから計算された固有値と比べて,ランダムなデータセットよりも大きい固有値までを採用しようという考えのようです。こうすることでサンプリングの誤差に対応できるとのことです。初出はHorn (1965)です。
Rでの実験
Rで平行分析を行うにはpsychパッケージのfa.parallelという関数を用いれば良いのですが,ここでは原理を理解するためにパッケージを使わずにやってみます。使うデータはpsych所収のbfiというデータセットです。ビッグファイブの性格特性の質問紙データで,各因子5項目ずつ計25項目の質問紙のデータです。26列目以降は回答者の属性に関するデータが入っています。サンプルサイズは2800です。
library(psych)
dat <- bfi[,1:25]
head(dat)
A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 E1 E2 E3 E4 E5 N1 N2 N3 N4 N5 O1 O2 O3 O4 O5
61617 2 4 3 4 4 2 3 3 4 4 3 3 3 4 4 3 4 2 2 3 3 6 3 4 3
61618 2 4 5 2 5 5 4 4 3 4 1 1 6 4 3 3 3 3 5 5 4 2 4 3 3
61620 5 4 5 4 4 4 5 4 2 5 2 4 4 4 5 4 5 4 2 3 4 2 5 5 2
61621 4 4 6 5 5 4 4 3 5 5 5 3 4 4 4 2 5 2 4 1 3 3 4 3 5
61622 2 3 3 4 5 4 4 5 3 2 2 2 5 4 5 2 3 4 4 3 3 3 4 3 3
61623 6 6 5 6 5 6 6 6 1 3 2 1 6 5 6 3 5 2 2 3 4 3 5 6 1まずは,元データからスクリープロットを描いてみます(15因子目まで)。
R_original <- cor(dat, use="pairwise.complete.obs")
e_original <- eigen(R_original)
plot(1:15, e_original$values[1:15], type="b")
abline(h=1)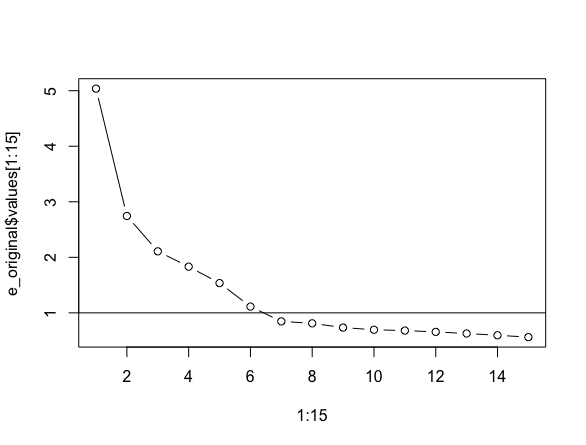
固有値が1より大きいという基準(Kaiser基準)でいくと6因子が適当のようです。
ここから平行分析をやってみます。まず,データセットと同じサイズのランダムデータを用意します。2800行,25列の乱数を標準正規分布から発生させて,そこから相関行列を計算します。計算された相関行列を固有値分解して固有値のベクトルを得ます。
random <- matrix(rnorm(nrow(dat)*ncol(dat),0,1), nrow(dat), ncol(dat))
e_random <- eigen(cor(random))ランダムデータから作られた固有値を先ほどの図に重ねてみます。
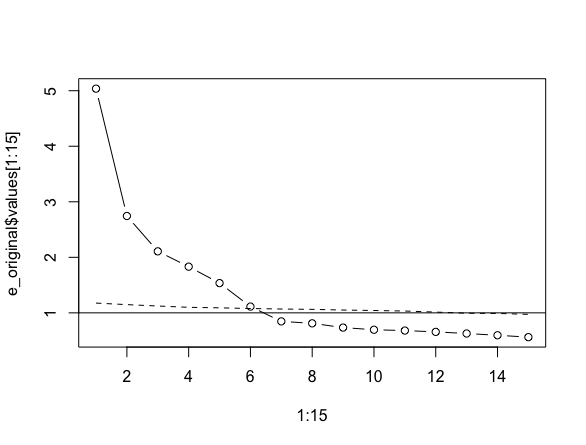
図中の点線が新たに作ったデータセットから得た固有値です。この点線の固有値と実際のデータの固有値を比べて,実際のデータの固有値の方が大きいところまで(図中だと6因子)を因子数として採択するというのが平行分析の考え方です。
ところで,ここで得られたランダムデータからの固有値は,サンプリングによるランダムな変動によりたまたま大きかったり,小さかったりするということがあるかもしれません。 そこで,ランダムデータを繰り返し発生させて,その平均の固有値との比較をしようという発想が出てきます。先ほどの手続きを50回繰り返して,その平均をとってみます。
niter <- 50
result <- matrix(NA, nrow=niter, ncol=ncol(dat))
for (iter in 1:niter){
random <- matrix(rnorm(nrow(dat)*ncol(dat),0,1), nrow(dat), ncol(dat))
result[iter, ] <- eigen(cor(random))$values
}
rand_eigval_mean <- apply(result, 2, mean)最終的に得た平均の固有値とオリジナルデータを比べたものが次の図です。
plot(1:15, e_original$values[1:15], type="b")
points(1:15, rand_eigval_mean[1:15], type="l", lty=2)
abline(h=1)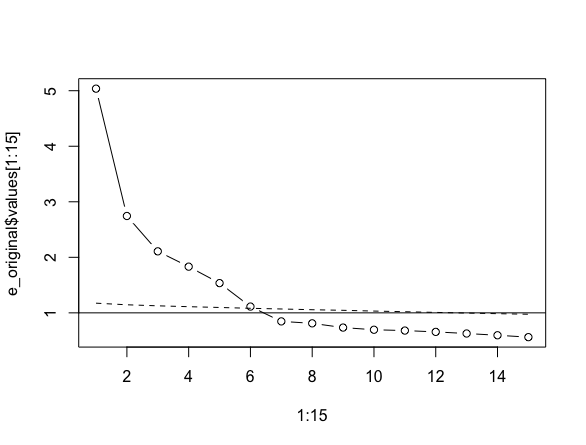
psychのfa.parallel関数
なお,この手続きはpsychのfa.parallel関数を使えば一行でできます。
fa.parallel(dat)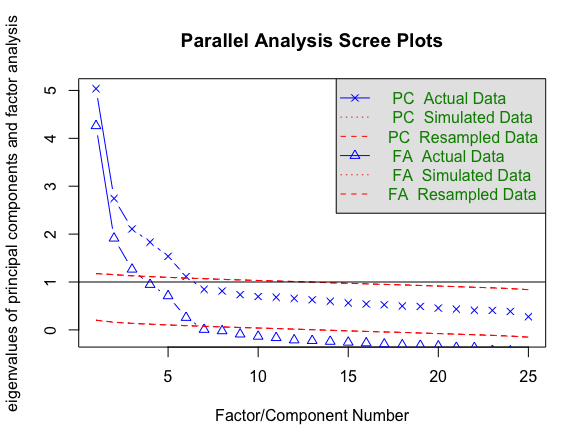
関数のヘルプをみると繰り返しのデフォルトは20回のようですが,n.iterの引数に回数を指定すれば増やすこともできるようです。
<ここから2020/9/24追記>
対角SMCによる方法
ところで,上でおこなった平行分析は主成分分析の結果に基づくものですが,Humphreys & Ilgen(1969)によって,主成分ではなく因子数の選択に適した方法が提案されています。
そこでは,サンプルの相関係数行列そのものから固有値を計算する代わりに,対角成分に共通性の推定値を代入した相関係数行列から固有値を計算します(この相関行列はreduced correlation matirxとも呼ばれたりしますが日本語訳をなんと言うのか知りません)。そして共通性の推定値には,ある変量とその他の変量の重みつきの合成変量の間の重相関係数の平方(squared multiple correlation; SMC)を用いる方法が知られています。
芝(1972)『因子分析法』によれば,この重相関係数は
$$ R^2 _{j \cdot n-1}=1-\frac{1}{r^{(-1)} _{jj}} $$
で求められるとのことです(p.166)。ここで$r^{(-1)} _{jj}$は元の相関行列の逆行列のj番目の対角成分を表しています。この式を用いることで,もとの相関係数の逆行列さえ求めまれば簡単に共通性の推定値が得られることになります。実際にRでやってみましょう。
smc <- 1 - (1/diag(solve(R_original)))
R_smc <- R_original
diag(R_smc) <- smc
e_smc <- eigen(R_smc)$values比較のために,対角SMCと対角1のものとを重ねてプロットしてみます。青い線の方が対角SMCのものです。
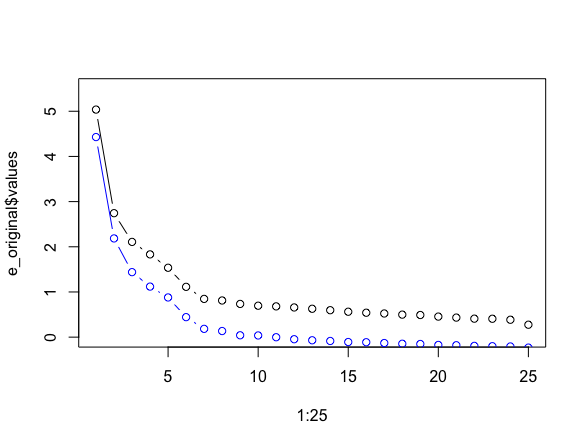
先ほどと同様に同じサイズのランダムデータをたくさん生成します。ランダムデータの相関行列からやはりSMCを計算し,それを対角成分に入れてから固有値を計算します。
niter <- 50
result <- matrix(NA, nrow=niter, ncol=ncol(dat))
for (iter in 1:niter){
random <- matrix(rnorm(nrow(dat)*ncol(dat),0,1), nrow(dat), ncol(dat))
random_cor<- cor(random)
smc_rand <- 1- (1/diag(solve(random_cor)))
diag(random_cor) <- smc_rand
result[iter, ] <- eigen(random_cor)$values
}
rand_eigval_mean <- apply(result, 2, mean)これを先ほどのプロットに重ねてみたものがこちら。対角SMCによる方法では8因子までを推奨しています。
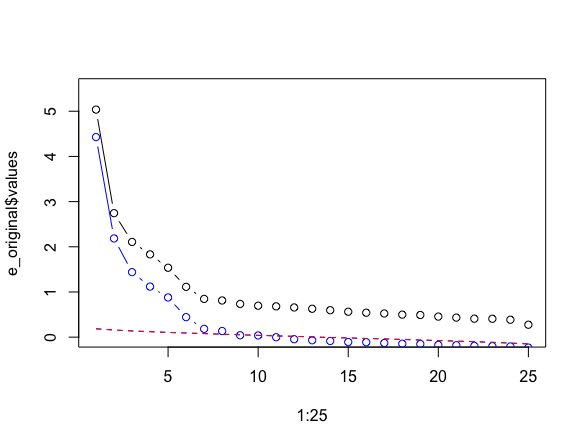
ちなみにpsychのfa.parallel()関数でやる場合には引数にSMC=Tとすると同じ結果が得られます。
<2020/9/24追記ここまで>