テトラコリック相関係数を求める関数の自作

Wednesday, June 19, 2019

Rでの関数化

作った関数は以下の通り。引数には2×2の相関表を指定する。途中のテトラコリック関数（？）で何次まで計算するかということをorder=という引数で指定する。デフォルトは論文に掲載されていたものと同じ6にしてある。

tetrachoric <- function(cor.table, order=6){

  #必要な数値を代入
  N <- sum(cor.table)
  prop.bd <- colSums(prop.table(cor.table))[2]
  prop.cd <- rowSums(prop.table(cor.table))[2]
  h <- qnorm(prop.bd, lower.tail = F)
  H <- dnorm(h)
  k <- qnorm(prop.cd, lower.tail = F)
  K <- dnorm(k)
  tau <- numeric(order)
  theta <- numeric(order)
  v_bar <- numeric(order)
  w_bar <- numeric(order)

  #テトラコリック関数
  for(n in 1:order){
    if(n==1){
      v_bar[n] <- h
      w_bar[n] <- k
      tau[n] <- H
      theta[n] <- K
    } else if (n==2){
      v_bar[n] <- h^2-1
      w_bar[n] <- k^2-1
      tau[n] <- H*h/sqrt(2)
      theta[n] <- K*k/sqrt(2)
    } else {
      v_bar[n] <- h * v_bar[n-1] - (n-1) * v_bar[n-2]
      w_bar[n] <- k * w_bar[n-1] - (n-1) * w_bar[n-2]
      tau[n] <-  H*v_bar[n-1]/sqrt(factorial(n))
      theta[n] <- K*w_bar[n-1]/sqrt(factorial(n))
    }
  }

  # 相関を計算
  coef_vec <- c(prop.bd * prop.cd - cor.table[2,2]/N, tau * theta)
  res <- Re(polyroot(coef_vec)[1])
  return(res)
}

性能評価の数値実験

この関数がどの程度正確に相関係数を推定できるか実験してみる。母相関を0.8とする2変量標準正規分布からN=1000の乱数を発生させて, それを $ h=0.3, k=-0.2 $ の閾値でそれぞれ2値化する。たとえば, 身長と体重の2変量が, それぞれ【高い,低い】【重い,軽い】のように2値データとして手に入った状態を想定すると良い。

library(mvtnorm)
dat <- rmvnorm(1000, mean=c(0,0), sigma=matrix(c(1,0.8,0.8,1),2,2))
height <- cut(dat[,1], breaks=c(-Inf,0.3,Inf),labels=c("低い", "高い"))
weight <- cut(dat[,2], breaks=c(-Inf,-0.2,Inf),labels=c("軽い", "重い"))

# こんな感じの相関表になる

table(height, weight)
      weight
height 軽い 重い
  低い  400  237
  高い   27  336

このような2値データのペアの相関係数を計算すると当然離散化前より絶対値が低下していることがわかるが, テトラコリック相関係数ではもとの値に近い値を推定できている。

cor(dat[,1], dat[,2]) # 離散化前の相関
[1] 0.7930115
cor(as.numeric(height),as.numeric(weight)) # 離散化後の相関
[1] 0.4956164
tetrachoric(table(height, weight)) # テトラコリック相関
[1] 0.7463495

さて, これと同様の手続きを10000回繰り返し, テトラコリック相関係数はどの程度もとの相関を再現できるかを以下のコードで確かめた。

## 繰り返しの回数
n.iteration <- 10000

##保存用ベクトル
tetra <- numeric(n.iteration)
cont <- numeric(n.iteration)
pearson <- numeric(n.iteration)

for(ite in 1:n.iteration){
  dat <- rmvnorm(1000, mean=c(0,0), sigma=matrix(c(1,0.8,0.8,1),2,2))
  height <- cut(dat[,1], breaks=c(-Inf,0.3,Inf),labels=c("低い", "高い"))
  weight <- cut(dat[,2], breaks=c(-Inf,-0.2,Inf),labels=c("軽い", "重い"))

  cont[ite] <- cor(dat)[2,1]
  pearson[ite] <- cor(as.numeric(height),as.numeric(weight))
  tetra[ite] <- tetrachoric(table(height, weight))  
}

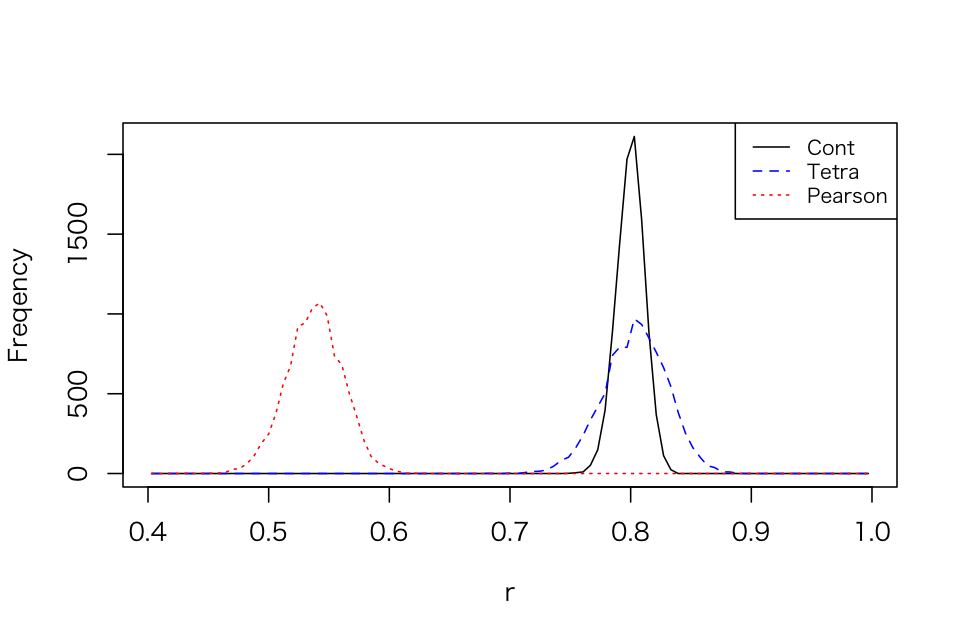
結果は次の画像の通りである。数値実験結果

図中のContというのが連続変量のまま相関係数を計算したもの, Pearsonが離散化した変数でそのままピアソンの積率相関を求めたもの, Tetraがテトラコリック相関係数を求めたものである。TetraとPearsonを比べると, Pearsonが0.5-06付近まで相関係数の絶対値が低下しているのに対して, Tetraは母相関である0.8のあたりを概ね正確に推定していることがわかる。

テトラコリック相関係数を求める関数の自作

Tags:

Categories:

Rでの関数化

性能評価の数値実験