EFAから計算したωとCFAから計算したω
2つのω係数について
信頼性係数の1つであるω係数は$\omega_h$と$\omega_t$があって,それぞれ
$$ \omega_h = \frac{{\bf 1^{\prime} c c^{\prime} 1}}{{\rm Var}(X)} \\ \omega_t = \frac{{\bf 1^{\prime} c c^{\prime} 1}+{\bf 1^{\prime} A A^{\prime} 1}}{{\rm Var}(X)} $$
として表される。${\bf c}$は一般因子の因子負荷量ベクトルで,${\bf A}$は群因子の因子負荷量行列である。
Revelle & Condon(2019)によると,これらの推定値を得る方法は,(1)EFAで高次因子モデルの因子負荷量を得てその結果にScmidt-Leiman変換をかける方法と,(2)CFAで直接的に双因子モデルを指定して推定値を得る方法がある。ここでは,Rで実際にその2つをやってみてどのような違いがあるかを検討する。
使うデータはPsychパッケージに入ってるThurstoneというデータ(相関行列)。9つのテストのデータで,3つの因子(1)Verbal Comprehension,(2)Word Fluency, (3)Reasoningにまとまるようである。サンプルサイズは213らしい。
https://www.personality-project.org/r/html/bifactor.html
探索的因子分析による方法
まずは,探索的因子分析でやってみる。psych所収のomega関数を使う。とても簡単。
library(lavaan)
library(psych)
library(knitr)
data("Thurstone")
res_efa <- omega(Thurstone)
kable(round(res_efa$schmid$sl,3))| g | F1* | F2* | F3* | h2 | u2 | p2 | |
|---|---|---|---|---|---|---|---|
| Sentences | 0.709 | 0.560 | -0.022 | 0.030 | 0.817 | 0.183 | 0.615 |
| Vocabulary | 0.726 | 0.553 | 0.042 | -0.022 | 0.835 | 0.165 | 0.631 |
| Sent.Completion | 0.683 | 0.521 | 0.020 | 0.004 | 0.738 | 0.262 | 0.632 |
| First.Letters | 0.646 | -0.001 | 0.558 | 0.002 | 0.729 | 0.271 | 0.573 |
| Four.Letter.Words | 0.622 | -0.011 | 0.489 | 0.076 | 0.632 | 0.368 | 0.613 |
| Suffixes | 0.558 | 0.112 | 0.409 | -0.060 | 0.495 | 0.505 | 0.629 |
| Letter.Series | 0.587 | 0.019 | -0.009 | 0.617 | 0.725 | 0.275 | 0.475 |
| Pedigrees | 0.577 | 0.238 | -0.033 | 0.339 | 0.505 | 0.495 | 0.659 |
| Letter.Group | 0.541 | -0.037 | 0.139 | 0.459 | 0.524 | 0.476 | 0.558 |
次のようなパス図も一緒に吐き出す。
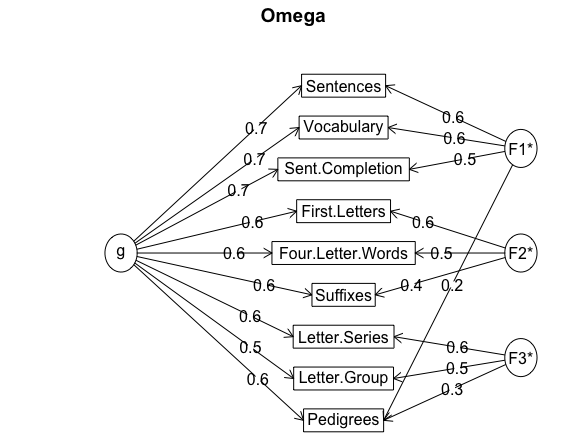
ω係数は,$\omega_h = 0.74$と$\omega_t = 0.93$とのことである。
Total, General and Subset omega for each subset
g F1* F2* F3*
Omega total for total scores and subscales 0.93 0.92 0.83 0.79
Omega general for total scores and subscales 0.74 0.58 0.50 0.47
Omega group for total scores and subscales 0.16 0.34 0.32 0.32これは先ほどの,SL変換後の因子負荷量から式通りに計算すると出てくる値である。
VarX <- sum(Thurstone)
c <- res_efa$schmid$sl[,"g"]
A <- res_efa$schmid$sl[,c("F1*","F2*","F3*")]
nume1 <- sum(c %*% t(c)) + sum(A %*% t(A))
nume2 <- sum(c %*% t(c))
nume1/VarX
#[1] 0.9308199
nume2/VarX
#[1] 0.7360703確認的因子分析による方法
続いて確認的因子分析による方法を試してみる。lavaanでCFAをして因子負荷量行列を取り出す。
mo <-"
g =~ Sentences+Vocabulary+Sent.Completion+First.Letters+Four.Letter.Words+Suffixes+Letter.Series+Pedigrees+Letter.Group
F1 =~ Sentences+Vocabulary+Sent.Completion
F2 =~ First.Letters+Four.Letter.Words+Suffixes
F3 =~ Letter.Series+Pedigrees+Letter.Group
"
res_cfa <- cfa(mo, sample.cov=Thurstone, orthogonal=T, sample.nobs = 213)
lambda <- inspect(res_cfa,what="std")$lambda
kable(round(lambda,3))| g | F1 | F2 | F3 | |
|---|---|---|---|---|
| Sentences | 0.768 | 0.488 | 0.000 | 0.000 |
| Vocabulary | 0.791 | 0.452 | 0.000 | 0.000 |
| Sent.Completion | 0.754 | 0.404 | 0.000 | 0.000 |
| First.Letters | 0.608 | 0.000 | 0.614 | 0.000 |
| Four.Letter.Words | 0.597 | 0.000 | 0.506 | 0.000 |
| Suffixes | 0.572 | 0.000 | 0.394 | 0.000 |
| Letter.Series | 0.567 | 0.000 | 0.000 | 0.727 |
| Pedigrees | 0.662 | 0.000 | 0.000 | 0.247 |
| Letter.Group | 0.530 | 0.000 | 0.000 | 0.409 |
この推定値を使って,先ほどと同様にωを計算する。
c <- lambda[,"g"]
A <- lambda[,c("F1","F2","F3")]
nume1 <- sum(c %*% t(c)) + sum(A %*% t(A))
nume2 <- sum(c %*% t(c))
nume1/VarX
#[1] 0.9278556
nume2/VarX
#[1] 0.7891304ω係数は,$\omega_h = 0.79$と$\omega_t = 0.93$とのことである。$\omega_h$については,EFAで計算した場合より若干高い値である。 この結果は,Revelle & Condon(2019)が次のように言っている通り。
The bifactor solution (g) tends to produce slightly larger estimates than the Schmid-Leiman procedure(h) because it forces all the cross loadings of the lower level factors to be 0 (p.9).
omegaSem関数について
ところでpsychにはomegaSemという関数があり,直接的に確認的因子分析に基づくωを計算できるようである。
omegaSem(Thurstone, n.obs=213)
Total, General and Subset omega for each subset
g F1* F2* F3*
Omega total for total scores and subscales 0.93 0.92 0.82 0.80
Omega general for total scores and subscales 0.79 0.69 0.48 0.50
Omega group for total scores and subscales 0.14 0.23 0.35 0.31関数の中身をしっかり覗いた訳ではないから詳しくは分からないが,どうやらomega関数でSL変換による因子負荷量を得たあとに,その因子負荷量をもとにlavaanのモデル式を自動で書き出して,lavaanに突っ込んでいるようである。お手軽だけれどもCFAのモデルが変なモデルになっていないか確認しないと痛い目をみそうである(もっともomegaSem関数を使うとパス図が描かれるからそこでチェックすれば良いだけの話だけど)
参考
Revelle, W., & Condon, D. M. (2019, August 5). Reliability From α to ω: A Tutorial. Psychological Assessment. Advance online publication. http://dx.doi.org/10.1037/pas0000754